Binary heap, heapsort and priority queues

In general the heap is a tree data structure. There are two different types of heaps, min-heap and max-heap.

In a min-heap each node is smaller or equal to its children and in a max-heap each node is greater than or equal to its children.

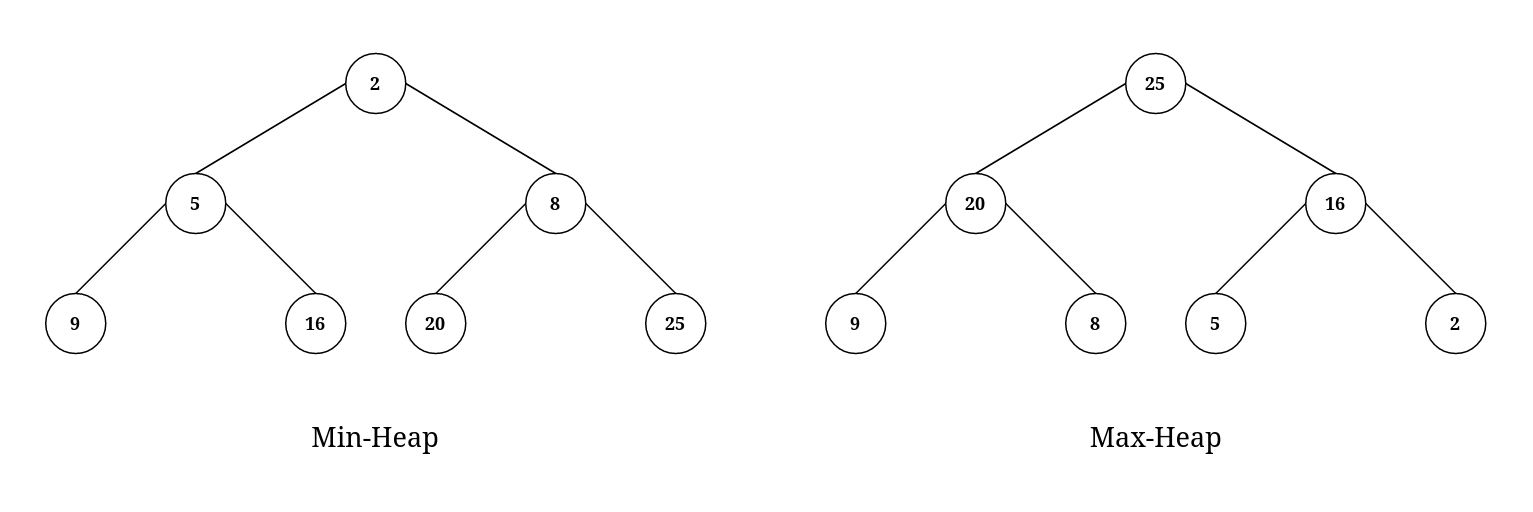
In a min-heap and max-heap we know that the root is the smallest or greatest element respectively. The time complexity of extracting the root element is $O(1)$.

Binary heap

A binary heap respects two properties:

Complete binary tree: A binary tree where every layer is filled except maybe the last one which must have all its elements as far to the left as possible.

Heap property: Each node is smaller or equal to its children if it is a min-heap and each node is greater or equal to its children if it is a max-heap.

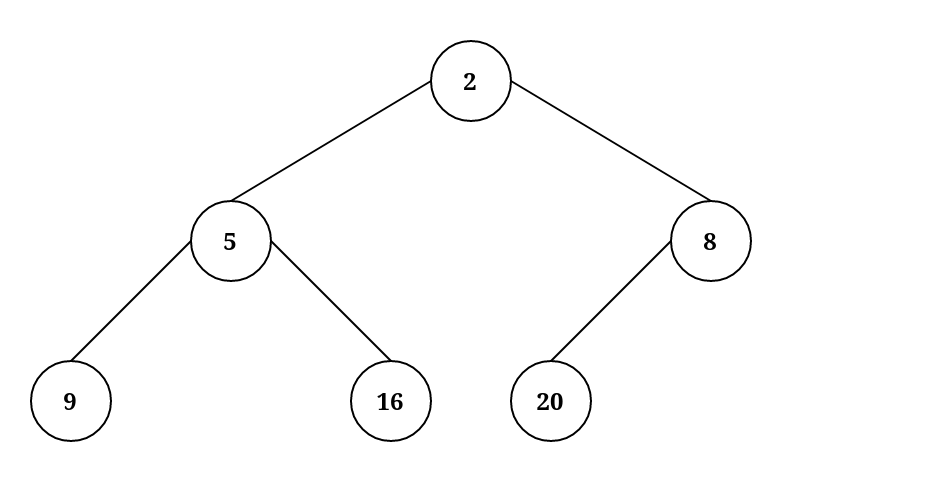
Here are two examples of invalid binary-heaps:

Storing the binary heap in an array

Since a binary heap is a complete binary tree it is possible to store the tree inside an array, which is more efficient. This is possible because the related nodes can be found based on the current node index.

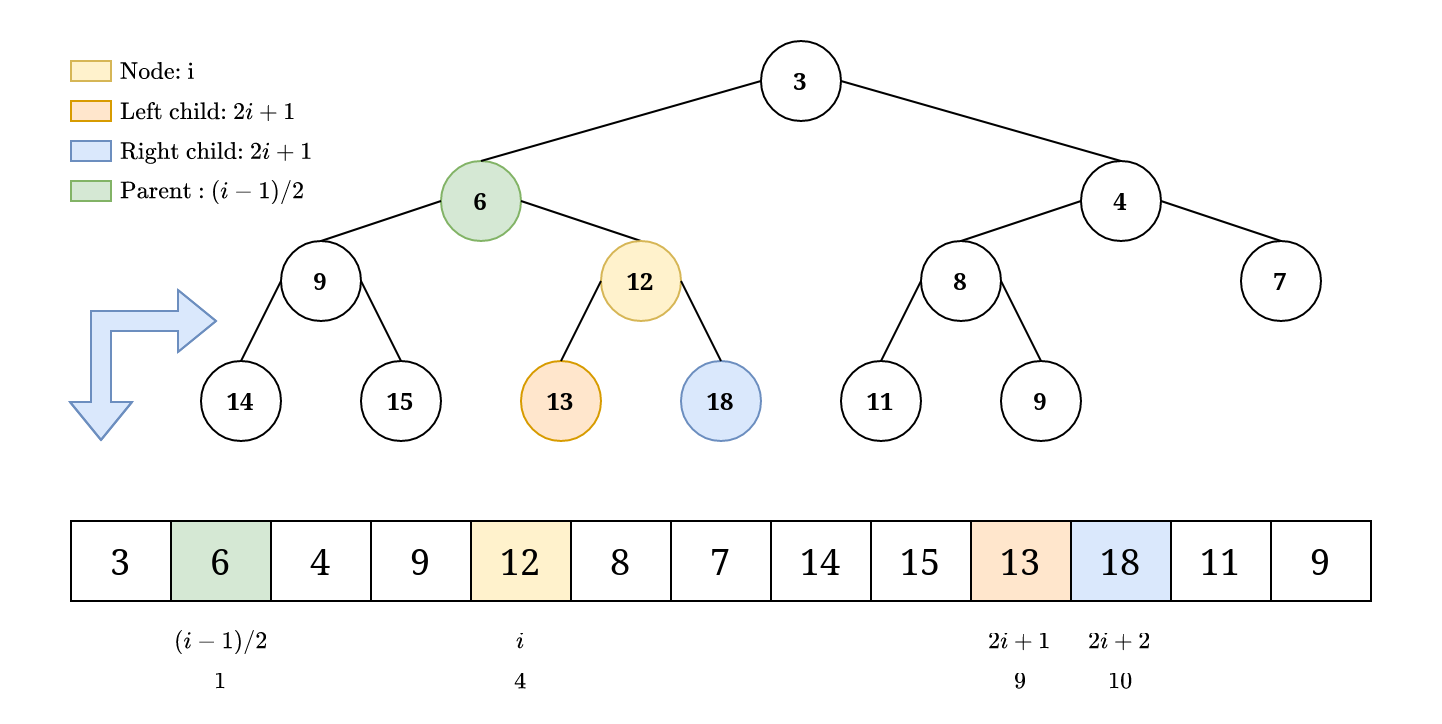
Binary heap operations

There are five main operations a binary heap needs to be able to handle.

Insert	Get min/max	Extract min/max	Update	Build
$O(log(n))$	$O(1)$	$O(log(n))$	With index$\\$ $O(log(n))\\$ Without $O(n)$	$O(n)$

In order to keep the heap property two more operations are needed, sift-up and sift-down.

Sift-up: When the node that we want to reposition is at the bottom sift-up is used. The sift-up operation swaps the element with its parent if it is smaller than its parent. It stops when the parent is larger.

Sift-down: When the node that we want to reposition is at the root sift-down is used. Sift-down checks its children and swaps if the children is smaller than itself. It stops when both children are larger.

Both of these operations moves the node by one level in the heap each iteration. This means that the number of iterations depend on the height of the heap. Since a binary heap is a complete tree and complete trees are always balanced, the time complexity of both of these iterations are $O(log(n))$.

Insert

To insert a new element into the heap place the element in the end of the array. This might break the heap property, therefore the sift-up operation is applied to the element. The time complexity of the insert operation is therefore $O(log(n))$.

Get min/max

To get the min/max from a heap is very efficient, since the target value will always be the root node. The time complexity of this operation is $O(1)$.

Extract min/max

To extract the min/max from a heap swap the root and end node of the heap. Now pop the end node and apply sift-down to the root node. The time complexity of this operation is $O(log(n))$ due to the sift-down operation.

Update

There are two scenarios when considering the update operation. If the index of the node is available or not. If the index is available, compare the updated value with the new value to determine whether to sift-up or sift-down. This takes $O(log(n))$ due to sifting.

If the index is not available the node first have to be found before comparing and sifting. To find the node takes $O(n)$ and therefore the complexity of the operation without the index of the node is also $O(n)$.

Build/Heapify

Most optimal way of building a heap is to traverse the list backwards and sift-down the elements. Because there are more nodes close to the bottom compared to the top it is better to use sift-down. Starting from the bottom avoids sifting down the same node later. The time complexity is $O(n)$ and here is the explanation:

The number of nodes at each level $l$ from the bottom up is roughly $\frac{n}{2^l}$ and the cost to sift-down the nodes is $l - 1$.

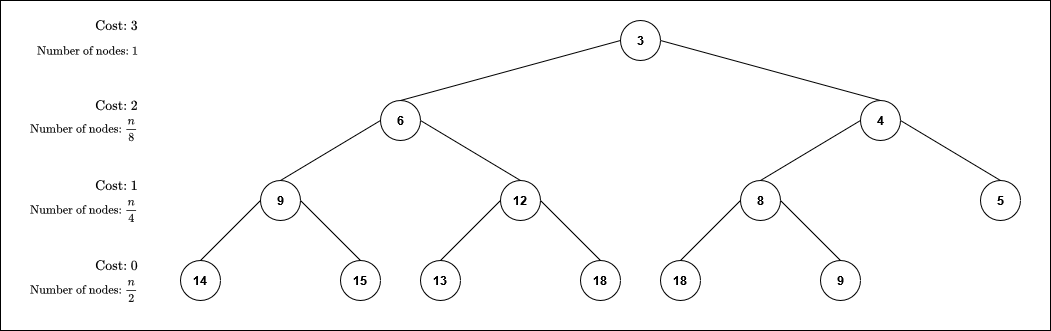
The total cost of building the heap is therefore

$$\begin{align} T(n) =& 0 \cdot \frac{n}{2} + 1 \cdot \frac{n}{4} + 2 \cdot \frac{n}{8} + 3 \cdot \frac{n}{16} + \ldots + ((\log_2{n} - 1) \cdot 1) \\ =& \sum^{\log_2{n-1}}_{k=0}{k \cdot \frac{n}{2^{k+1}}} = \frac{n}{4} \sum^{\log_2{n-1}}_{k=0}{k \cdot \frac{1}{2^{k-1}}} \lt \frac{n}{4} \sum^{\infty}_{k=0}{k \cdot \frac{1}{2^{k-1}}} \end{align}$$

The last sum in equation 2 is an upper bound and we will continue studying this sum

$$\begin{align} \frac{n}{4} \sum^{\infty}_{k=0}{k \cdot \frac{1}{2^{k-1}}} = \frac{n}{4} \sum^{\infty}_{k=0}{k \cdot \frac{1^{k-1}}{2^{k-1}}} = \frac{n}{4} \sum^{\infty}_{k=0}{k \left(\frac{1}{2}\right)^{k-1}} \end{align}$$

We can now set $x = \frac{1}{2}$ and we get

$$\begin{align} \frac{n}{4} \sum^{\infty}_{k=0}{k x^{k-1}} =& \frac{n}{4} \cdot \frac{d}{dx}\left[\sum^{\infty}_{k=0}{x^k}\right] = \frac{n}{4} \cdot \frac{d}{dx}\left[\frac{1}{1-x}\right] \\ =& \frac{n}{4} \cdot \frac{1}{(1-x)^2} = \frac{n}{4} \cdot \frac{1}{(1-1/2)^2} \\ =& \frac{n}{4} \cdot \frac{1}{1/4} = n = O(n) \end{align}$$

Applications

Heap Sort

A sorting algorithm that heapifies the array and then extracts it until it becomes empty. Even though heapify takes $O(n)$ the algorithm still needs to extract $n$ elements. One extraction takes $O(\log(n))$ which means that extracting $n$ elements takes $O(n\log{n})$ and the time complexity of this algorithm is therefore $O(n \log{n})$.

Priority Queue

A queue data structure that stores the node with the highest priority in the front of the queue. A priority queue has five main operations:

Enqueue	Dequeue	Peek	Change priority	Is empty
$O(\log{n})$	$O(\log{n})$	$O(1)$	With index$\\$ $O(log(n))\\$ Without $O(n)$	$O(1)$